Otisni knjiguOtisni knjigu

Brojevni sustavi

Sjedište: CARNET Loomen LMS
E-kolegij: Pripreme za ispit iz informatike na DM 2022
Knjiga: Brojevni sustavi
Otisnuo/la: Gost (anonimni korisnik)
Datum: srijeda, 22. listopada 2025., 13:48

Opis

Kratak pregled brojevnih sustava vezanih uz računalo

Sadržaj

1. Binarni i heksadekadski brojevni sustav

Oba navedena brojevna sustava pripadaju u pozicijske brojevne sustave, što znači da mjesto znamenke u broju određuje njezinu vrijednost.

Svaki pozicijski brojevni sustav ima bazu i znamenke. Baza brojevnog sustava predstavlja broj znamenaka u tom sustavu. Najmanja znamenka svakog sustava je 0, dok je najveća znamenka za jedan manja od baze.

Brojevni sustavi vezani uz računalo su sustavi koji imaju veze sa brojem 2:

  • Binarni (baza 2)
  • Oktalni (baza 8 =>23)
  • Heksadekadski (baza 16 => 24)
Kurikulumom nastave informatike predviđeno je poznavanje binarnih i heksadekadskih sustava, pa ćemo se u daljnjem radu baviti s njima.
Binarni brojevni sustav

Baza binarnog brojevnog sustava je 2. Znamenke su dvije: 0 i 1.

Kako broj 101 može biti broj u bilo kojem brojevnom sustavu, ukoliko nije u dekadskom i ne piše u kojem je sustavu, pored njega ćemo u indeks staviti bazu.

Primjer:

Broj 101 je broj u dekadskom brojevnom sustavu.
Broj 101(2) je broj u binarnom brojevnom sustavu.

Heksadekadski brojevni sustav

Baza ovog brojevnog sustavu je 16

Znamenke su: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15.

Kako bi u zapisu brojeva znali radi li se o znamenki, npr. 12 ili kombinaciji znamenaka 1 i 2, znamenke od 10 do 15 ćemo zapisivati velikim slovima A, B, C, D, E i F.

vrijednost

prikaz

10 A
11 B
12 C
13 D
14 E
15 F

1.1. Pretvorba dekadskoga broja u binarni

Pretvorba dekadskog broja u broj prikazan u binarnome brojevnom sustavu:

  • Dekadski broj dijeli se s bazom (broj 2).
  • Postupak se ponavlja sa svakim kvocijentom sve dok se ne dobije kvocijent 0.
  • Prilikom svakog dijeljenja nastaju ostaci (0 ili 1).
  • Zapisivanjem ostataka od posljednjeg prema prvom dobije se zapis dekadskog broja u binarnom brojevnome sustavu.
Napomena: Ovaj postupak primjenjuje se za prikaz dekadskoga broja u bilo kojoj bazi! Broj se dijeli s bazom, a ostaci su iz brojevi iz intervala od 0 do b-1 (b je baza).

Primjer:


Preporuka

Jednostavniji način za pretvorbu dekadskoga broja u binarni, prikladniji za rješavanje zadataka u ispitima DM je korištenje potencija broja dva i činjenice da su binarni i dekadski brojevni sustavi pozicijski brojevni sustavi.

Ovaj je postupak najlakše objasniti primjerom:


Što smo napravili? S lijeva u desno smo raspisali potencije broja 2. Zatim smo pogledali koja od tih potencija nam je potrebna kako bi njihovim zbrajanjem dobili broj 67:

Kako je 67 = 64 + 2 + 1, ispod tih potencija upišemo znamenku 1, a ispod ostalih znamenku 0. I dobili smo naš binarni broj!




1.2. Pretvorba binarnoga broja u dekadski

Pretvorba broja zapisanog u nekoj bazi u dekadski broj odvija se preko težinskih vrijednosti znamenaka. Svaka se znamenka pomnoži s potencijama baze, idući s desna na lijevo. Krajnja desna potencija je nula. 

Preporuka: Kako bi izbjegli zabune s težinskim vrijednostima znamenki koristite logiku iz prethodne lekcije. Iznad znamenki binarnoga broja zapišite potencije broja dva i jednostavno zbrojite one potencije ispod kojih je zapisana znamenka 1.

Primjer:



1.3. Brojevi s decimalnom točkom

Kod pretvorbe brojeva s decimalnom točkom desno od decimalne točke zapisuju se negativne potencije broja 2!
Podsjetimo se!
 2-1 = 0.5,
2-2= 0.25,
2-3= 0.125...

Pogledajte primjer:


1.4. Pretvorba heksadekadskog broja u binarni i obrnuto

Pretvorba heksadekadskog broja u binarni

Heksadekadski broj pretvorit ćemo u binarni tako da svaku heksadekadsku znamenku prikažemo pomoću četiri binarne.

Kako znamo kojom kombinacijom binarnih znamenki ćemo zamijeniti određenu heksadekadsku znamenku?

Možemo koristiti istu logiku kao u dekadskom brojevnom sustavu. Prikažimo heksadekadsku znamenku kao kombinaciju potencija broja 2. Na primjer, znamenku 11 možemo zapisati kao 1*23+0*22+1*21+1*20=1011(2).

Primjer:

Prikažimo heksadekadski broj 174A u binarnom brojevnom sustavu:
174A(16)=0001 0111 0100 1010 (2)

Pretvorba binarnog broja u heksadekadski

Binarni broj pretvaramo u heksadekadski tako da, krenuvši od desna na lijevo, odvajamo po četiri binarne znamenke. Svaku skupinu od po četiri binarne znamenke pretvorimo u jednu heksadekadsku znamenku. Ukoliko nam "nedostaje" binarnih znamenki, nadopunimo ih s lijeve strane broja. Za pretvorbu koristimo jednaku logiku  kao i u prethodnoj pretvorbi. Na primjer, 1011(2)=8+2+1=11(16)=B.

Primjer:

Prikažimo binarni broj 100010001 u heksadekadskom brojevnom sustavu.

Uzmemo li skupine od po četiri znamenke naš broj sada izgleda ovako: 0001 0101 1001(2) (crvene znamenke su nadopunjene zbog nedostatka znamenaka). Zapišemo ispod svake skupine brojeve 8, 4, 2 i 1:

0 0 0 1   0 1 0 1   1 0 0 1
8 4 2 1   8 4 2 1   8 4 2 1
   1             5              9

U svakoj skupini zbrojimo one vrijednosti iznad kojih piše broj 1 i dobijemo rješenje:
101011001(2)=159(16).

 

1.5. Pretvorba heksadekadskoga broja u dekadski i obrnuto

Iako za pretvorbu dekadskoga broja u heksadekadski možemo koristiti standardni postupak dijeljenje sa 16 i zapisivanja ostataka, a za pretvorbu heksadekadskoga broja u dekadski težinske vrijednosti znamenki brže je i jednostavnije ove pretvorbe raditi preko binarnoga brojevnoga sustava! Heksadekadski broj pretvorite u binarni, pa binarni u dekadski i obrnuto! Na taj način izbjegavate množenje i dijeljenje te cijeli postupak svodite na zbrajanje potencija broja 2.

S obzirom na činjenicu da na ispitu DM ne možete koristiti kalkulator, ovo je lakši način rješavanja ovakvih zadataka.

2. Zbrajanje binarnih brojeva

Zbrajanje u binarnom sustavu provodi se jednako kao zbrajanje u dekadskom brojevnom sustavu, s tim da se prijenos pojavljuje već u situaciji kad zbrajamo znamenke 1 i 1. Jer 1+1=2, a znamenka 2 ne postoji u binarnom brojevnom sustavu.

Tako vrijedi:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 0 i 1 "dalje" (1 prijenos)

Primjer 1: Potrebno je binarno zbrojiti brojeve  1101110(2) i 10011(2).

 

Rješenje:        

1

1

1

1

1

1

 

 

prijenos

 

1

1

0

1

1

1

0

 

+

 

 

1

0

0

1

1

 

1

0

0

0

0

0

0

1

 

 

Provjera:

1101110(2)=

 

1

1

0

     10011(2)=

+

 

1

9

10000001(2) =

 

1

2

9

3. Pitanja s provedenih ispita

  1. (Ogledni primjerak testa za državnu maturu) Prikažite broj (BABA)16 u binarnom brojevnom sustavu.
     
  2. (Primjer testa za državnu maturu, 2008.) Što je od navedenoga binarni zapis dekadskoga broja 23.125?
     a) 11101.001
     b) 10111.1111101
     c) 10111.001
     d) 10111.1011111
     
  3. (Primjer testa za državnu maturu, 2008.) Heksadekadski prikaz nekog broja je 5A. Koji je dekadski ekvivalent tog broja?
     a) 510
     b) 45
     c) 90
     d) 180
     
  4. (Probna državna matura, 2009.) Koji je dekadski zapis binarnoga broja 101,11?
    a) 5,75
    b) 3,75
    c) 5,3
    d) 3,3
     
  5. (Probna državna matura, 2009.) Koji je heksadekadski zapis dekadskoga broja 58?
    a) A3
    b) E2
    c) 3A
    d) 2E
     
  6. (Probna državna matura, 2009.) Koji je binarni zapis broja (1234)16?

  7. (Državna matura, 2010, ljetni rok, zadatak 14)  Koji je binarni zapis heksadekadskoga broja BCDE?
     a) 1011110011011110
     b) 1011110110111110
     c) 1100101111011110
     d) 1110110111001011
  8. (Državna matura, 2010, ljetni rok, zadatak 31) Koji je binarni zapis broja (536B)16?

  9. (Državna matura, 2010, jesenski rok, zadatak 12) Koji je binarni zapis dekadskoga broja 6,75?
      a) 10,1001011
     b) 10,11
     c) 110,1001011
     d) 110,11
  10. (Državna matura, 2010, jesenski rok, zadatak 13) Koji je heksadekadski zapis binarnoga broja 1101011,01?
     a) D6,8
     b) 1AD
     c) 107,25
     d) 6B,4
  11. (Državna matura, 2010, jesenski rok, zadatak 31) Koji je binarni zapis broja (9E7D)16?
  12. (Državna matura, 2011, ljetni rok, zadatak 15) Koji je broj u heksadekadskome sustavu neposredni sljedbenik heksadekadskoga broja 9F?
     a) 100
     b) 910
     c) A0
     d) A10
  13. (Državna matura, 2011, jesenski rok, zadatak 15) Kako se u heksadekadskome obliku zapisuje neposredni prethodnik broja (200)16?
     a) 100
     b) 1FF
     c) 199
     d) 201
  14. (Državna matura, 2011, jesenski rok, zadatak 31) Koliko znamenaka „0” ima broj (3887)16 kada je zapisan u binarnome brojevnome sustavu (ako se prilikom zapisivanja ne zapisuje vodeće nule)?
  15. (Državna matura, 2012, ljetni rok, zadatak 9) Koji je heksadekadski ekvivalent dekadskog broja 257?
     a) A01
     b) 101
     c) 110
     d) 10A
  16. (Državna matura, 2012, ljetni rok, zadatak 25) Koji je heksadekadski zapis binarnog broja 110101101,11?
  17. (Državna matura, 2012, jesenski rok, zadatak 9) Koji je heksadekadski ekvivalent dekadskog broja 254?
     a) FE
     b) EF
     c) EE
     d) FF
  18. (Državna matura, 2012, jesenski rok, zadatak 11) Koji je rezultat zbrajanja binarnih brojeva 111101 i 101111?
     a) 1101100
     b) 1001100
     c) 1011101
     d) 1110111
  19. (Državna matura, 2012,jesenski rok, zadatak 23) Napišite binarni zapis dekadskog broja 17,375.
  20. (Državna matura, 2012, jesenski rok, zadatak 25) Koliko znamenaka „1” ima broj ED37(16) kada je zapisan u binarnom brojevnom sustavu?
  21. (Državna matura, 2013, ljetni rok, zadatak 9) Koji je heksadekadski zapis dekadskoga broja 40?
     a) 28
     b) 64
     c) 82
     d) 128
  22. (Državna matura, 2013, ljetni rok, zadatak 10) Koji je dekadski zapis binarnoga broja 101,11?
     a) 5,75
     b) 5,3
     c) 4,75
     d) 4,3
  23. (Državna matura, 2013, ljetni rok, zadatak 25) Koji je heksadekadski zapis binarnoga broja 101010010100,01?
  24. (Državna matura, 2013, jesenski rok, zadatak 10) Koji je heksadekadski zapis binarnoga broja 10110110000,1?
     a) 5B0,1
     b) B60,8
     c) B6,1
     d) 5B0,8
  25. (Državna matura, 2013, jesenski rok, zadatak 25) Koji je dekadski zapis binarnoga broja 101101,01?
  26. (Državna matura, 2014, ljetni rok, zadatak 9) Koji je rezultat zbrajanja binarnih brojeva 1011101 i 1101110?
     a) 1001011
     b) 11001011
     c) 10110011
     d) 10111011
  27. (Državna matura, 2014, ljetni rok, zadatak 10) Koji je heksadekadski zapis broja 1100,1012?
     a) A,5
     b) C,5
     c) C,A
     d) 14,A
  28. (Državna matura, 2014, ljetni rok, zadatak 23) Napišite binarni zapis dekadskoga broja 26,125.
  29. (Državna matura, 2014, ljetni rok, zadatak 24) Koliko znamenaka „0” ima broj 9AC3(16) kada je zapisan u binarnome brojevnom sustavu?
  30. (Državna matura, 2014, jesenski rok, zadatak 9) Koji je rezultat zbrajanja binarnih brojeva 1101101 i 101010?
     a) 11000001
     b) 10000001
     c) 11010111
     d) 10010111
  31. (Državna matura, 2014, jesenski rok, zadatak 10) Koji je broj u heksadekadskome brojevnom sustavu točno dvostruko veći od dekadskoga broja 86?
     a) C
     b) AC
     c) CA
     d) 172
  32. (Državna matura, 2014, jesenski rok, zadatak 23) Napišite binarni zapis dekadskoga broja 19,375.
  33. (Državna matura, 2014, jesenski rok, zadatak 24) Koliko znamenaka „1” ima broj 4725(8) kada je zapisan u binarnome brojevnom sustavu?
  34. (2015, ljetni rok, zadatak 9) Koji je binarni zapis dekadskoga broja 29(10)?
    A. 1011
    B. 1101
    C. 10111
    D. 11101
  35. (2015, ljetni rok, zadatak 10) Koji je binarni zapis heksadekadskoga broja E01,3(16)?
    A. 111000000001,0011
    B. 11101,11
    C. 111000000001,11
    D. 110001,0011

  36. (2015, jesenski rok, zadatak 9) Koji je heksadekadski zapis dekadskoga broja 30(10)?
    A. E1
    B. 1E
    C. E
    D. 48

  37. (2015, jesenski rok, zadatak 10)Koji je binarni zapis dekadskoga broja 25,5(10)?
    A. 10011,1
    B. 11001,01
    C. 11001,1
    D. 10011,01

  38. (2015, jesenski rok, zadatak 25) Koji je heksadekadski zapis binarnoga broja 11111101011,101(2)?

  39. (2016., ljetni rok, zadatak 9) Koji je rezultat zbrajanja binarnih brojeva 1101011 i 10101110?
    A. 11001
    B. 10011001
    C. 100011001
    D. 110000100
  40. (2016., ljetni rok, zadatak 10) Kako glasi broj 1110,01112 zapisan u heksadekadskome brojevnom sustavu?
    A. 7,7
    B. E,E
    C. 7,E
    D. E,7

  41. (2016., ljetni rok, zadatak 12) Koji od navedenih brojeva ima najveću dekadsku vrijednost?
    A. 53(16)
    B. 1010001(2)
    C. 01010100(2)
    D. 82(10)

  42. (2016., ljetni rok, zadatak 23)  Koji je binarni zapis dekadskoga broja 21,125?

  43. (2016., ljetni rok, zadatak 24)  Koliko se puta pojavljuje niz znamenaka „011” u broju ABCD16 kada je zapisan u binarnome brojevnom sustavu?

  44. (2022., ljetni rok, zadatak 6)  Web-stranica skole.hr ima brojčanu IPv4 adresu http://193.198.184.184/. Koji je binarni zapis te adrese?
    A. 11000101.11001010.10111000.10110100
    B. 11000001.11000110.10111000.10111000
    C. 11000101.11000110.10110100.10110100
    D. 11000001.11001010.10111000.10111000

  45. (2022., ljetni rok, zadatak 7) Na nekoj web-stranici otvorili smo opciju Alati za razvojne programere i ustanovili
    da se koriste različitim bojama koje su zapisane heksadekadski. Željeli bismo odabranom bojom s te web-stranice obojiti tekst u MS Wordu.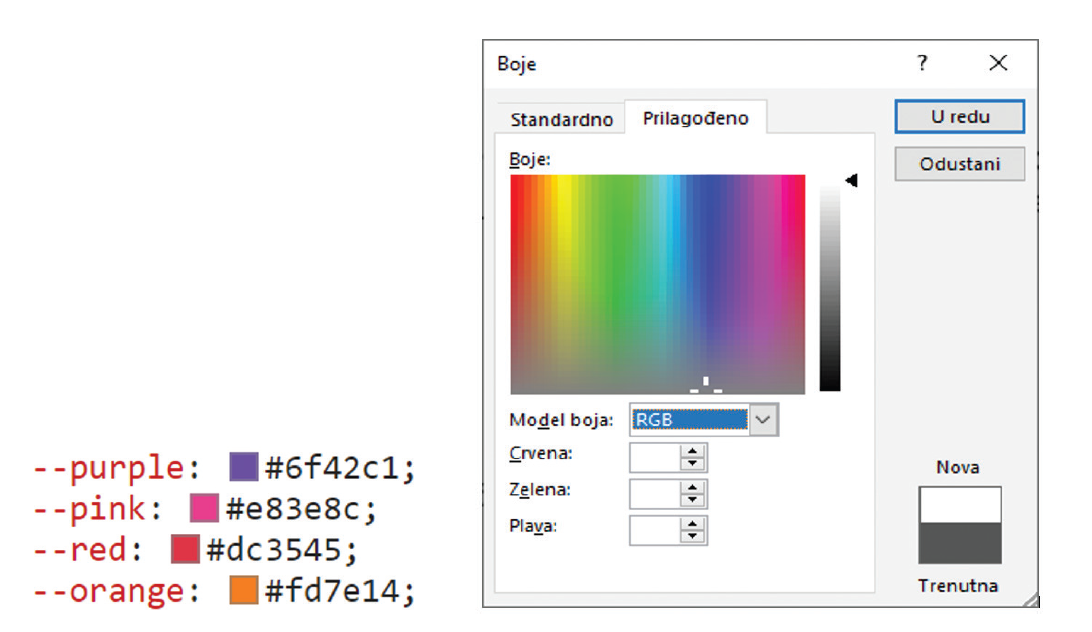

    Pročitali smo heksadekadsku vrijednost crvene boje (red). Ta je vrijednost #dc3545, što znači da su crvena = dc16, zelena = 3516 i plava = 4516.
    Koje dekadske vrijednosti trebamo unijeti za crvenu, zelenu i plavu boju da bi tekst postao baš te nijanse crvene boje?
    A. crvena: 22010, zelena: 5310 i plava: 6910
    B. crvena: 11310, zelena: 5310 i plava: 19110
    C. crvena: 22010, zelena: 6810 i plava: 19510
    D. crvena: 11310, zelena: 6210 i plava: 6910


3.1. Rješenja

  1. 1011101010111010
  2. C
  3. C
  4. A
  5. C
  6. 1001000110100
  7. A
  8. 101001101101011
  9. D
  10. D
  11. 1001111001111101
  12. C
  13. B
  14. 7
  15. B
  16. 1AD,C
  17. A
  18. A
  19. 10001,011
  20. 11 (1110110100110111)
  21. A
  22. A
  23. A94,4
  24. D
  25. 45,25
  26. B
  27. C
  28. 11010,001
  29. 8 (1001101011000011)
  30. D
  31. B
  32. 10011,011
  33. 7 (100111010101) 
  34. D
  35. A
  36. B
  37. C
  38. 7EB.A
  39. C
  40. D
  41. C
  42. 10101,001
  43. 2
  44. B
  45. A